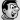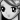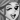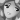李  锐

北京中国计量科学研究院长度处 100013

 

    齿轮测量中心是八十年代逐渐发展起来的齿轮测量设备。设备采用坐标测量的原理，应用数控技术和计算机技术，具有使用方便、快捷高效、多参数、多用途等特点。用于这些优势，在与传统的机械式齿轮量仪的市场竞争中很快占据了优势。近年来随着精密机械产品价格的不断升高和数控技术的发展完善，一高一低的变化使机械式齿轮量仪基本上退出了市场，特别是高端市场。

    齿轮测量中心除了上述优点外，还有测量重复性好，受环境影响比机械式量仪小等特点，因此齿轮中心出具的数据可信的程度比较高。但是，对于齿轮中心究竟有多大的示值误差，人们的看法却并不相同，本文将对此问题进行探讨。

    因为误差只能在测量过程的各个环节中带进来，因此研究齿轮中心的测量误差，首先要看齿轮中心的测量结果是怎样得出来的。

    齿轮中心使用了坐标测量的原理，测量结果全部来自测量采点的坐标，测量点坐标值的准确程度就决定了测量结果的准确程度。另一个带入误差的过程是数据处理的过程，根据德国PTB的研究，坐标测量过程中数据处理带入的误差不能忽略，但我们目前的工作尚未作到这样细致的程度，软件带入的误差不在本文的讨论范围以内。

    齿轮中心的坐标系一般由一个回转坐标（主轴）和按主轴的径向、切向和轴向三个互为垂直的直线坐标组成，测量时各轴在数控系统控制下使测量传感器贴被测量面运动，完成测量数据的采集。以典型的圆柱齿轮测量为例，在测量齿廓类参数时使用回转坐标与切向坐标，测量齿向参数时使用回转坐标与轴向坐标，测量齿距类参数时与测量齿廓类参数时相同。

下面以齿向测量为例进行测量误差的分析。

在齿向参数的测量中，齿轮中心测得回转坐标值θ和轴向坐标值H，由此可以计算得出导程P，进而得出任意圆上的螺旋角β。螺旋角与导程的关系可由下式表达：

                         

式中β--螺旋角, R--半径，θ--转角， P--导程。

（1）     
式还可以表达为：

即在半径R一定时，螺旋角β是转角θ和导程P的函数。为研究测量中θ与P的测量误差对β的影响，可以对β求偏微分：

容易得到误差传递系数

    比较困难的是如何确定设备的测角误差和测长误差。这两项误差与多种因素相关，如设备的整体布局、部件制造精度、仪器的调整状态、传感器的制造精度和安装调整状态、环境影响等等。由于没有方便简洁的方法作出相应的评价，所以需要根据仪器的设计布局、单项误差的测量结果等进行分析估计，一般要考虑到下列因素的影响：

影响测角精度的因素有：轴系的偏摆、轴系与测角传感器的安装偏心、测角传感器的制造误差、主轴顶尖的制造误差和安装误差、上顶尖的偏摆和位置误差、工件的安装误差、测量传感器的示值误差等；

影响测长精度的因素有导轨的位置误差、测长传感器的制造误差和安装误差、阿贝差、测量传感器的示值误差、环境温度的影响等。

确定了误差分量的数量后，根据生产商提供的数据或实测的单项误差数据，可以求得各误差分量的标准差，经合成得到最后测量结果的标准差。正常情况下，齿轮中心测量齿廓类和齿向类公差项目时，标准差（k＝1）一般不应大于1μm。

对以上误差分析的过程、误差传递系数c1和c2、各误差分量所占比重等进行研究，我们不难得到下面的推论：

1．                   从（4）式和（5）式中可以看到，误差传递系数是半径R、转角θ和导程P的函数，这说明仪器在不同的位置测量或是测量不同的工件时，测量结果的示值误差是不一样的。

2．                   测量不同精度等级的工件时，示值误差也不相同，这是由于精度较低的工件和工装带来较大的安装误差，同时数据处理对测量曲线的大幅波动也比较敏感。

3．                   设备的调整状态和工作的环境将会影响到示值误差。

以上分析说明使用齿轮测量中心可以得到较小的测量误差，有较高的工作效率，但并不能消除仪器的示值误差，因此在涉及齿轮协作加工的验收时，不同的仪器出具的测试报告会有所不同，对于高精度的齿轮产品，尤其要注意测量设备的量值一致，必要时应在测量前使用标准器校准仪器，修正仪器的示值误差。